서포트벡터머신(SVM)은 모델 성능도 좋고 선형, 비선형 분류, 회귀, 이상치 탐색 등에 다목적으로 사용할 수 있는 강력한 ML모델이다.
SVM 개념
SVM은 결정경계(Decision Boundary)를 정의하는 모델이다.

위 그림에서 실선은 빨간색, 파란색 두 개의 클래스를 정확하게 분류한다. 선 밖에 새로운 훈련 샘플이 추가되어도 결정경계에는 전혀 영향을 미치지 못하지만 경계에 걸쳐있는 샘플은 그렇지 않다. 점선에 걸쳐있는 샘플들은 boundary가 더 밖으로 밀려나게끔 한다.
이렇게 결정경계에 위치해서 Boundary에 결정적인 영향을 미치는 샘플을 서포트 백터라고 부르며, 결정경계와 서포트 백터 사이의 거리를 Margin(마진)이라고 한다.

위 그래프에서 클래스를 분류하는 결정 경계 중 어떤 것이 가장 이상적일까? 당연히 초록색 선이다. 노란색 선은 파란색 클래스에 너무 가깝고 파란색 선은 주황색 클래스에 너무 가깝다. 두 클래스와 거리가 가장 먼 decision boundary가 가장 이상적으로 최적의 결정경계는 마진을 최대화한다. 그렇기 때문에 SVM을 라지 마진 분류라고도 한다.
모든 샘플이 결정 경계 바깥쪽에 올바르게 분류되어 있는 것을 하드 마진 분류라고 한다. 그런데, 하드 마진 분류는 어떠한 아웃라이어도 허용하지 않기 때문에 데이터가 선형적으로 구분될 수 있어야만 제대로 작동하며 이상치에 민감하다는 문제점이 있다.

이렇게 이상치가 있는 경우에는 하드 마진을 아예 찾을 수 없다. 현실의 데이터에서 이러한 문제를 피하기 위해서는 보다 더 유연한 모델인 소프트 마진 분류가 필요하다. 소프트 마진 분류는 위와 같은 이상치를 어느정도 허용하면서 마진을 가능한 한 넓게 유지한다.
사이킷런 SVM 주요 파라미터
| 파라미터 | default | 설명 |
| C | 1.0 | 오류를 얼마나 허용할 것인지 (규제항) 클수록 하드마진, 작을수록 소프트마진에 가까움 |
| kernel | 'rbf' (가우시안 커널) | 'linear', 'poly', 'rbf', 'sigmoid', 'precomputed' |
| degree | 3 | 다항식 커널의 차수 결정 |
| gamma | 'scale' | 결정경계를 얼마나 유연하게 그릴지 결정 클수록 오버피팅 발생 가능성 높아짐 |
| coef0 | 0.0 | 다항식 커널에 있는 상수항 r |
사이킷런에서는 파라미터 C를 이용해서 SVM 모델이 오류를 얼마나 허용할 것인지 조정할 수 있다. C값이 클수록 하드마진에 가깝고 작을수록 소프트마진에 가깝다. 다만 C값이 너무 크면 오버피팅, 너무 작으면 언더피팅이 발생할 수 있으므로 적정값을 찾아야 한다.
kernel은 데이터 셋의 형태에 따라 다르다. 선형 데이터셋의 경우 'linear'를, 비선형 데이터셋은 'poly(다항식)', 'rbf(가우시안)'을 주로 사용한다. 다항식 커널은 degree로 차수를 지정해줘야 하며 rbf커널이라면 gamma와 C값 조정이 필수적이다.
어떤 커널을 사용할지 고민된다면 일단은 선형 커널부터 시도해보는게 좋다. 훈련 세트가 너무 크지 않다면 RBF 커널도 좋다. 사실 가장 좋은건 교차검증과 그리드 탐색으로 최적의 커널을 찾는 것이다.
★같이 읽어보면 좋은 글
gamma는 학습데이터에 얼마나 민감하게 반응할 것이냐를 정하는 것으로 C와 비슷한 규제 파라미터이다. gamma값이 높으면 학습데이터 의존도가 높아 과적합이 발생하기 쉽다.
coef0은 모델이 높은 차수와 낮은 차수에 얼마나 영향을 받을지 조정하는 파라미터이다. 과대적합이라면 다항식의 차수를 줄이고, 과소적합이라면 차수를 늘려야 한다.
다항식 커널
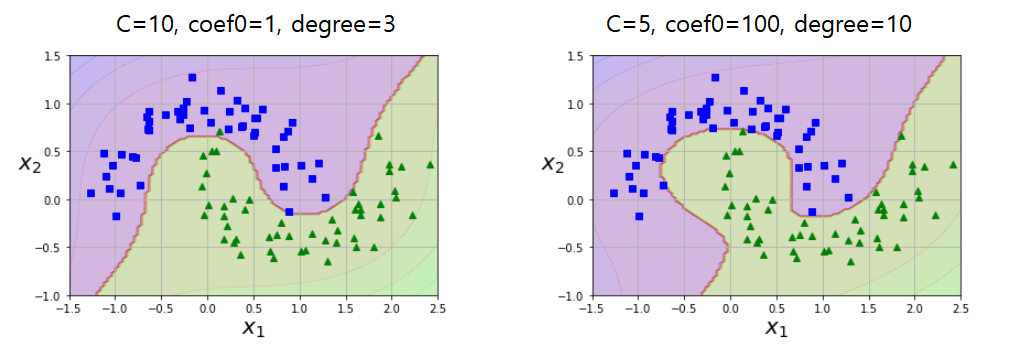
다항식(polynomial)커널에서 C, coef0, degree를 각각 달리했을 때의 결정경계 모습이다. 차수가 높고 규제가 적은 오른쪽 모델이 더 타이트하게 경계가 그려졌다.
rbf (가우시안) 커널

gamma와 C값을 바꾸어 rbf커널 모델을 훈련시켜봤다. gamma값이 커지면 보라색 영역이 좁아지고 결정경계도 더 구불구불하고 복잡해진다. 반대로 gamma값이 작으면 결정경계가 훨씬 단순하고 부드럽다.
다만 gamma값이 너무 크면 오버피팅이 발생할 수 있다. gamma=5인 경우는 오버피팅이 우려되고 r=0.1, C=0.001인 경우는 훈련 세트를 거의 분류하지 못해 언더피팅된 상태이다. 위의 4개의 케이스 중에서는 gamma=0.1, C=1000이 가장 이상적이라고 할 수 있다.
'파이썬 > 머신러닝' 카테고리의 다른 글
| 차원 축소 PCA(주성분 분석) 기본 개념 - 투영과 매니폴드 학습 (0) | 2021.08.01 |
|---|---|
| 차원의 저주 개념, 발생 원인과 해결 방법 (2) | 2021.08.01 |
| 경사하강법(Gradient Descent)과 learning_rate 조정의 중요성 (0) | 2021.07.25 |
| XG Boost 파이썬 이해하기 - 파라미터 정리 및 파이썬래퍼와 사이킷런래퍼 코드 실습 (1) | 2021.07.25 |
| K-최근접 이웃 (K-NN) 분류기, 가장 간단한 머신러닝 알고리즘 (0) | 2021.07.21 |



