경사하강법은 가장 일반적인 최적화 알고리즘이다.
gradient는 비용함수의 미분값으로, 경사하강법은 비용 함수를 최소화하기 위해 반복적으로 파라미터를 조정한다.

고등학교 때 미분 배웠던걸 생각해보자. 위와 같은 이차함수에서 편미분값=0이 되는 지점이 함수의 최소값이다.
마찬가지로 경사하강법도 임의의 초기값에서 시작해 학습스텝의 크기만큼 MSE가 감소되는 방향으로 진행해 최소값에 수렴할 때까지 파라미터를 조정한다. 이 때 학습 스텝의 크기가 매우 중요하다. 학습 스텝의 크기는 learning_rate 파라미터로 조정한다.

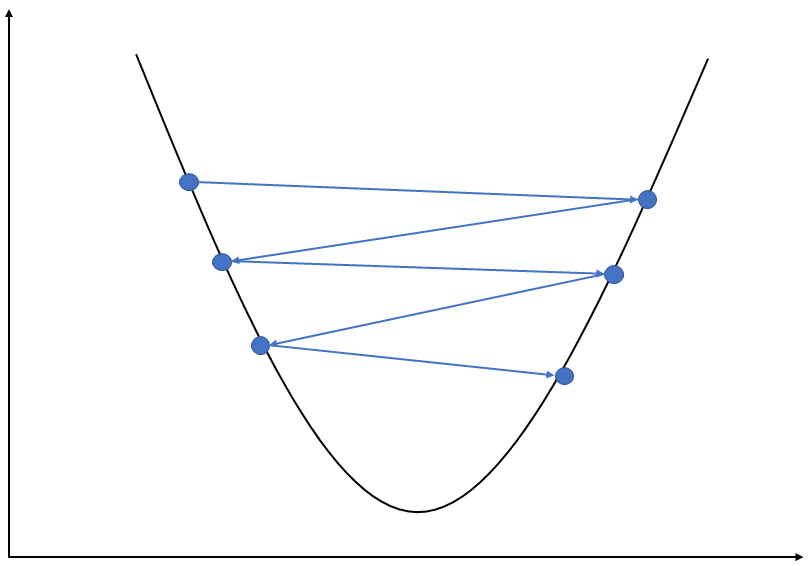
만약 learning_rate가 너무 작다면 알고리즘이 최소값에 수렴할 때까지 아주 오랜 시간이 걸릴 것이다. 반대로 learning_rate가 너무 크다면 점진적으로 하강하지 못하고 더 큰 값으로 발산해서 최소값을 찾기 어려울 수 있다.
또 하나의 어려운 점은 모든 비용함수가 2차함수처럼 깔끔한 형태가 아니라는 점이다.

이렇게 복잡한 형태의 비용함수라면 최소값을 찾기 어려워진다. 위와 같은 비용함수에서 무작위 알고리즘이 왼쪽부터 시작한다면 빨간색의 지역 최소값을 전역 최소값으로 착각하고 지역최소값에 도달할 수 있다.
*전역 최소값 : 전체 범위에서의 최소값
*지역 최소값 : 특정 범위 내에서의 최소값
다행히 선형회귀의 MSE 비용함수는 볼록함수이기 때문에 지역 최소값이 없어 learning_rate만 잘 조정하면 경사하강법으로 전역 최소값에 가깝게 도달할 수 있다.
경사하강법은 크게 배치 하강법과 확률적 하강법, 미니배치 세 가지로 나뉜다. 배치 경사 하강법은 모든 스텝에서 전체 훈련 세트를 사용해 편미분값을 계산하기 때문에 훈련 세트가 크면 속도가 아주 느리다.
반대로 확률적 경사하강법은 각 스텝에서 샘플 하나를 무작위로 선택하고 그 샘플의 편미분값을 계산하기 때문에 배치 경사하강법에 비해 훨씬 빠르다. 다만 무작위로 샘플링하는 것이기 때문에 배치 경사하강법보다 훨씬 불안정하다. 배치 경사하강법은 비용함수가 최소값에 도달할 때까지 스무스하게 감소하지만 확률적 경사하강법은 위아래로 요동치기 때문에 지역 최소값을 찾을 가능성이 높다.
이런 문제를 해결하기 위해서는 학습률을 점진적으로 감소시키면 된다. 처음에 시작할 때는 학습률을 크게 해서 지역 최소값에 빠지지 않게 하고 어느정도 학습이 진행되면 학습률을 감소시켜 전역 최소값에 도달하게 하는 것이다.
마지막으로 미니배치 경사하강법은 미니배치라고 부르는 임의의 작은 샘플 세트에 대해서 편미분값을 계산한다.

| 장점 | 단점 | |
| 배치 경사하강법 | 안정적, 전역 최소값을 찾을 확률이 높음 | 학습 속도가 오래 걸림 |
| 확률적 경사하강법 | 학습 속도가 빠름 | 배치보다 불안정, 지역최소값에 빠지기 쉬움 |
| 미니배치 경사하강법 | 학습 속도가 빠름 | 배치보다 불안정, 지역최소값에 빠지기 쉬움 |
추가로 세가지 모두 사이킷런의 SGDRegressor로 구현 가능하다.
'파이썬 > 머신러닝' 카테고리의 다른 글
| 차원의 저주 개념, 발생 원인과 해결 방법 (2) | 2021.08.01 |
|---|---|
| 서포트벡터머신(SVM) 개념과 주요 파라미터 정의 (0) | 2021.07.27 |
| XG Boost 파이썬 이해하기 - 파라미터 정리 및 파이썬래퍼와 사이킷런래퍼 코드 실습 (1) | 2021.07.25 |
| K-최근접 이웃 (K-NN) 분류기, 가장 간단한 머신러닝 알고리즘 (0) | 2021.07.21 |
| light GBM이란? 파라미터 설명과 코드 실습 (2) | 2021.07.11 |



