*이 글은 파이썬 라이브러리를 활용한 머신러닝 책을 기반으로 작성되었습니다.
분류기에서 예측의 불확실성을 추정하는 함수는 decision_function과 predict_proba 크게 두가지가 있다. 대부분의 분류 클래스가 두 함수(최소 한개)를 제공한다. 이진분류뿐만 아니라 다중 분류에도 사용할 수 있다.
예측을 만들어내는 것은 decision_function과 predict_proba 출력의 임계값을 검증하는 것인데, 이진탐색에서 임계값은 각각 0과 0.5이다.
이진 분류에서 decision_function 결과값은 n_samples이며 각 샘플이 하나의 실수 값을 반환한다. decision_function 값의 범위는 데이터와 모델 파라미터에 따라 달라진다.
반면, predict_proba는 각 클래스에 대한 확률이며 decision_function 보다 이해하기 쉽다. 확률값이기 때문에 항상 0과 1 사이의 값을 가지며 두 클래스의 확률 합은 항상 1이다.
사이킷런 load_iris 데이터셋에 GradientBoostingClassifier를 적합시켜 decision_function과 predict_proba 의 쓰임새를 알아보자.
import numpy as np
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.4, random_state=42)
X_test, X_val, y_test, y_val = train_test_split(X_test, y_test, test_size=0.5, random_state=42)
gbrt = GradientBoostingClassifier(learning_rate=0.01, random_state=42)
gbrt.fit(X_train, y_train)
print('결정 함수의 결과 형태: {}'.format(gbrt.decision_function(X_val).shape))
#결정함수 결과 중 앞에 일부분만 확인
print('결정 함수 결과:\n{}'.format(gbrt.decision_function(X_val)[:6,:]))
다중 분류에서 decision_function 의 결과값의 크기는 (n_samples, n_classes)이다. 위의 결과는 샘플이 30개, 클래스가 3개라고 해석할 수 있다.
두번째 결정함수 결과 값의 각 열은 각 클래스에 대한 확신 점수이다. 수치가 크면 해당 클래스에 속할 가능성이 높고, 수치가 작으면 가능성이 낮다. 여기서 첫번째 열은 2번 클래스, 두번째 열은 1번 클래스에 해당될 가능성이 높다고 해석할 수 있다.
print('가장 큰 결정 함수의 인덱스:\n{}'.format(np.argmax(gbrt.decision_function(X_val), axis=1)))
print('예측:\n{}'.format(gbrt.predict(X_val)))
각 포인트별 최대값의 인덱스와 예측값을 비교해볼 수도 있다.
추가로 보는 바와 같이 decision_function은 임의의 범위를 갖고 있다. 불균형 데이터에서 임계값을 바꾸면 더 좋은 결과를 얻을 수 있지만 범위가 정해져있지 않기 때문에 최적의 임계점을 고르는게 쉽지 않다.
반면 predict_proba 는 0과 1 사이 값으로 범위가 고정되어 있기 때문에 임계값 선택이 더 쉽고 결정 함수에 비해 해석도 더 용이하다.
print('예측 확률:\n{}'.format(gbrt.predict_proba(X_val)[:6]))
print('합: {}'.format(gbrt.predict_proba(X_val)[:6].sum(axis=1)))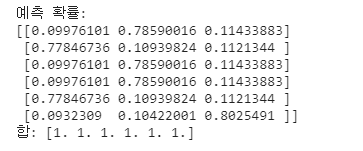
각 열의 합은 항상 1이며 값이 클수록 해당 클래스에 속할 확률이 높다.
정리
1. decision_function과 predict_proba 결과값의 크기는 항상 (n_samples, n_classes)
(**이진분류의 decision_function은 열이 하나, 양성 클래스에 대응하는 값을 가짐!)
2. predict_proba 결과값의 합은 항상 1, 범위는 항상 0~1(확률값)
3. decision_function은 임의의 범위
4. decision_function과 predict_proba 모두 값이 클수록 해당 클래스에 속할 확률이 높다.
'파이썬 > 파이썬 기초' 카테고리의 다른 글
| 편향(bias) 분산(variance) 트레이드 오프와 MSE (0) | 2021.07.18 |
|---|---|
| 지도 학습 분류와 회귀의 차이와 성능 평가 지표 (0) | 2021.07.18 |
| 파이썬 라이브러리 - numpy, pandas, matplotlib 등 기본 라이브러리 개념 (0) | 2021.07.17 |
| 빅데이터 분석 기사 자격증 파헤치기! 필기, 실기 시험 유형과 응시자격 (0) | 2021.07.17 |
| axis=1 뜻, 판다스 drop함수로 간단하게 알아보기 (0) | 2021.06.27 |



