지도학습에서 bias, variance는 에러 처리할 때 중요하게 생각해야 하는 요소이다.
bias(편향): 실제 값과 예측 값 간의 차이
variance(분산): 예측값이 흩어진 정도 (예측값의 평균과 예측값들 간의 차이)
둘다 손실(loss)이기 때문에 가능하면 bias, variance를 모두 작게 하는 것이 좋다.
하지만 기본적으로 편향과 분산은 트레이드오프 관계에 있다.

low bias, low variance가 가장 이상적인 모델이다.
그림의 첫번째 high bias, low variance는 언더피팅된 경우이다.
train data를 단순하게 학습하는 경우, 너무 적은 데이터로 학습하는 경우, 비선형 데이터에 선형 모델을 학습시키는 경우에는 underfitting이 발생하며 분산은 작은데 편향이 커지게 된다.
반대로 train data에 너무 잘맞게 모델을 학습시키면 오버피팅되면서 편향은 작은데 분산은 커지게 된다. 보통 노이즈가 많은 데이터로 학습하거나 파라미터가 많은 모델(ex.결정트리)을 사용하는 경우 오버피팅이 발생하기 쉽다.
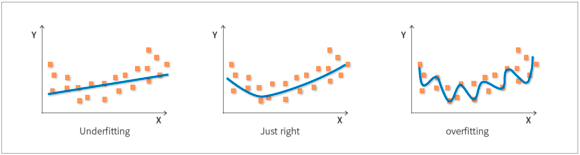
과소적합과 과대적합 모두 만든 모델로 test data를 예측하기 어렵기 때문에 좋은 모델이 아니다.
다만 bias와 variance는 trade-off 관계라서 하나를 줄이면 하나가 높아진다. 따라서 오류 최소화를 위해서는 편향과 분산의 합이 최소가 되는 적당한 지점을 찾는 것이 필요하다.
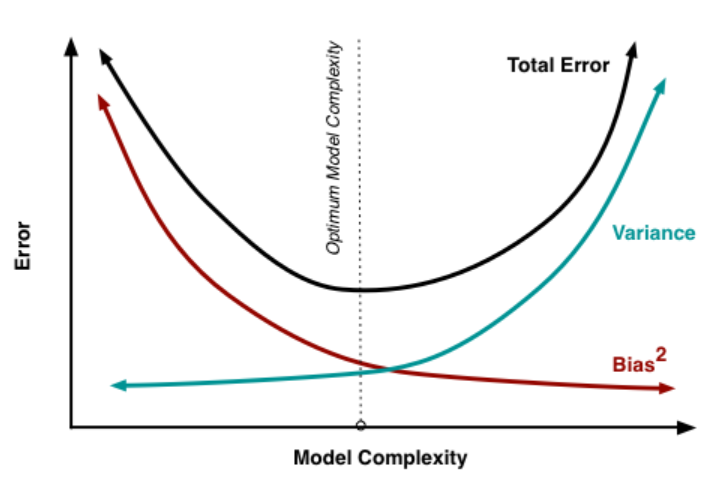
MSE는 total loss를 측정하는 지표이다.
MSE는 실제 값과 예측값의 차이, 즉 오차를 제곱해서 더한 후 평균을 낸 값으로 오차가 클수록 MSE도 커진다.

MSE는 분산, 편향의 제곱값, 노이즈의 합으로 이루어진다. 이때 노이즈는 데이터 자체의 한계로 인해 어떤 모델을 사용하든 줄일 수 없는 오차이다.
따라서 MSE값을 최소화하기 위해서는 결국 분산과 편향의 제곱의 합을 최소화하는 선에서 적당한 모델을 찾아야 하는 셈이다. 분산이 커지지 않도록 하기 위해서 L1규제, L2규제 등 다양한 규제 방법을 사용하게 된다. 릿지와 라쏘에 대해서는 다음 포스팅에서 보다 자세히 설명하겠다.
'파이썬 > 파이썬 기초' 카테고리의 다른 글
| 하이퍼파라미터와 파라미터의 차이 정확히 짚고 넘어가자 (0) | 2021.07.28 |
|---|---|
| 릿지 회귀, 오버피팅 방지를 위한 선형회귀 모델 규제 (0) | 2021.07.19 |
| 지도 학습 분류와 회귀의 차이와 성능 평가 지표 (0) | 2021.07.18 |
| 파이썬 라이브러리 - numpy, pandas, matplotlib 등 기본 라이브러리 개념 (0) | 2021.07.17 |
| 빅데이터 분석 기사 자격증 파헤치기! 필기, 실기 시험 유형과 응시자격 (0) | 2021.07.17 |



