연속확률변수(2) - t분포, F분포, 카이제곱분포

t분포, F분포, 카이제곱분포는 모두 정규분포에서 파생된 분포이다. 정규분포에서 생성된 표본 데이터 집합에 수식을 적용해서 값을 변화시키면 데이터 집합의 분포가 달라지는데 적용된 수식에 따라 t분포, F분포, 카이제곱 분포가 생성된다. 이 세 분포들은 모두 통계량 분포라고 불리며 가설 검정에 사용된다.


1. 카이제곱 분포
정규분포를 따르는 확률 변수 X의 k개의 서로 독립적인 표준 정규 확률변수를 제곱해서 더하면 양수값만을 갖는 분포가 된다. 이를 카이제곱 분포 χ2(x;k)라고 하며 카이제곱 분포는 자유도 k에 따라 형태가 달라진다. 범주형 자료 분석에 주로 사용된다.

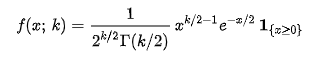
카이제곱 분포는 감마분포의 특수한 형태이며, E(X)=k, Var(X)=2k이다.

카이제곱분포는 기본적으로 좌측으로 치우친 분포인데 자유도 k가 커질수록 점점 대칭적으로 바뀐다. 자유도란 통계적 추정을 할 때 표본자료 중 모집단에 대한 정보를 주는독립적인 자료의 수를 의미한다.

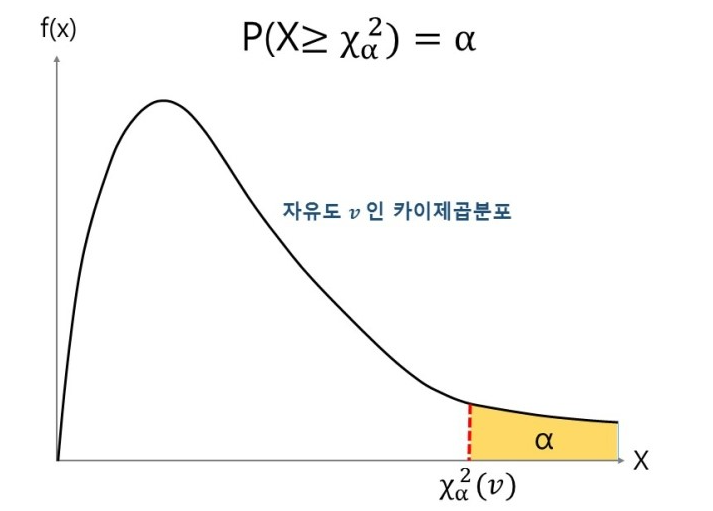
카이제곱 분포를 따르는 n개의 표본을 뽑고 이 n개의 확률표본을 전부 더했을 때 확률변수의 총합은 n이 무한대로 수렴할수록 중심극한정리에 따라 정규분포를 따르게 된다. 단, 주의할 점은 k가 충분히 크지 않은 경우 중심극한정리를 통해 곧바로 정규분포로 근사하면 오차가 많이 발생한다.


*중심극한정리
표본의 개수가 커지면 모집단의 분포와 상관없이 표본분포는 정규 분포에 근사해진다.



2. t-분포
t-분포는 정규분포의 평균을 측정할 때 주로 사용되는 분포이다.

t-분포는 위와 같은 새로운 확률변수 T를 정의한다. 확률변수 Z는 표준정규분포를 따르고 V는 자유도가 v인 카이제곱 분포를 따를 때, 서로 독립인 Z와 V에 대해 새로운 확률변수 T가 정의된다. 그리고 확률변수 T는 자유도가 v인 t분포를 따른다.


확률변수 T를 정의할 때 표준정규분포 Z가 들어있는데, Z를 찾기 위해서는 모집단의 분산을 알아야한다. 다만 모분산을 알려면 전수조사를 해야 하기 때문에 현실적으로 모분산을 알 수는 없다. 그렇기 때문에 모분산 대신 표본분산을 이용한다.


즉, t-분포는 모분산(혹은 표준편차)가 알려지지 않은 경우에 정규분포 대신 이용하는 확률분포라고 할 수 있다. 카이제곱분포와 마찬가지로 표본의 수가 많아질수록 중심극한 정리에 의해 정규분포에 수렴한다.

기댓값은 자유도가 1보다 클때 0이고 분산은 k/k-2이다.

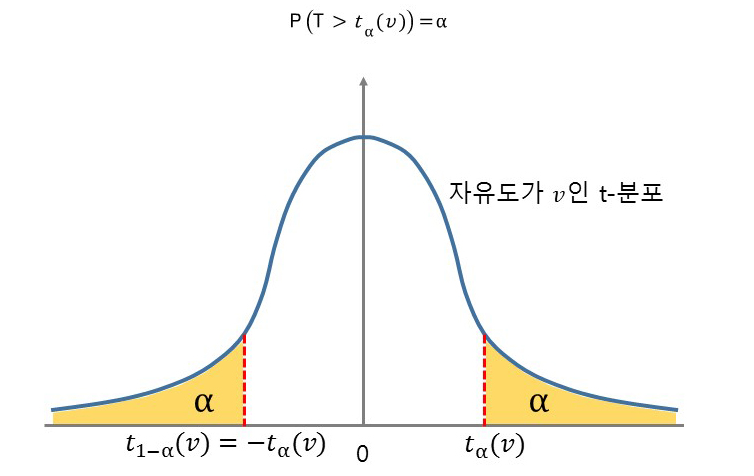
t-분포는 기본적으로 정규분포와 같은 종모양이며 t=0에서 좌우대칭을 이룬다. 자유도에 의해 t분포의 모양이 결정되며, 자유도가 커질수록 표준정규분포에 가까워진다. 보통 표본수가 30 이상이면 표준정규분포와 가깝다고 한다. 반대로 말하면 표본 크기가 30보다 작으면 t분포를 사용, 30보다 크면 표준정규분포를 사용하면 된다.

 

3. F-분포
F-분포는 정규분포를 이루는 모집단에서 독립적으로 추출한 표본들의 분산비율이 나타내는 연속확률분포이다. 독립적인 카이제곱 분포가 있을 때 두 확률 변수의 비율로, 두 집단 간 분산의 동일성 검정에 활용한다.

분산비율을 구한다는 말은 즉, 두 분산의 나눗셈을 확률분포로 나타낸다는 의미이다. 확률변수 F는 자유도가 (k1, k2)인 F-분포를 따른다.

카이제곱분포와 비슷하게 왼쪽으로 치우치고 오른쪽 꼬리가 긴 비대칭 형태이다. 두 집단의 분산을 서로 나눴을 때 1에 가까울수록 분산이 비슷하고 1에서 멀수록 분산이 다르다.


그래프에서 보는 바와 같이 표본의 수가 많아질수록 위로 뾰족한 정규분포와 비슷해진다.