이산확률분포(2) - 초기하분포, 기하분포, 음이항분포, 다항분포

2021.09.21 - [파이썬/빅분기] - 이산확률분포 - 이항분포와 포아송 분포

이산확률분포 - 이항분포와 포아송 분포

 

지난 포스팅에서는 이산확률분포의 가장 기본이 되는 분포인 베르누이 분포와 이항분포, 포아송 분포에 대해 살펴보았다. 이번 포스팅에서는 초기하분포, 기하분포, 음이항분포, 다항분포를 정리해보려 한다.

 

 

1. 초기하분포

초기하분포란 비복원추출에서 크기가 N인 모집단에서 표본을 n번 추출했을 때 원하는 것 k개가 뽑힐 확률의 분포이다. 중고등학생 때 확률을 배울 때 대표적인 문제였던 공 뽑기 문제를 생각하면 된다.

 

ex)

파란공과 빨간공이 5개씩 들어있는 주머니에서 5개의 공을 비복원 추출할 때 뽑은 공 중에서 2개는 파란공, 3개는 빨간 공일 확률을 구하기

 

 

만약 이 상황에서 비복원추출이 아니라 복원추출을 한다면 이항분포에 해당한다.

(비복원추출 → 초기하분포 / 복원추출 → 이항분포)

 

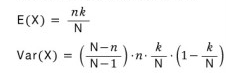
초기하분포의 분산에 있는 (1-k/N)이 바로 유한모집단수정항인데 이는 초기하분포가 비복원추출을 하기 때문에 모집단이 유한집단이 되어서 나타나는 항이다. k는 대체로 1보다 크기 때문에 유한모집단수정항은 1보다 작고, 초기하분포의 분산은 이항분포의 분산보다 작다.

 

 

만약 모집단인 N의 크기가 무한대에 가깝게 커지면 유한모집단수정항은 1에 가까워지면서 초기하분포의 분산은 이항분포의 분산과 근사하게 된다. 즉, 모집단의 크기가 무한대에 가깝게 커지면 비복원추출이라고 할지라도 복원추출과 다름없어진다.

 

 

2. 기하분포

기하분포는 베르누이 시행을 독립적으로 반복해서 처음으로 성공할 때까지 걸리는 시행한 횟수 k에 대한 분포이다.

 

 

 

성공확률인 p에 따른 기하분포인데 성공확률이 클수록 초반에 성공할 확률이 크고(=k가 작다), 성공확률이 작을 수록 초반에 성공할 확률이 작다(=k가 크다).

 

 

기하분포는 무기억성이라는 성질을 갖고 있다. 예를 들어 주사위를 던져서 처음으로 1이 나오는 확률을 구한다고 할 때, 10번을 던졌는데 1이 안나왔다고 해도 11번째 주사위를 던질 때 처음부터 던진 것보다 1이 나올 확률이 더 높아지는 것은 아니라는 것이다.

 

 

3. 음이항분포

기하분포와 같은 조건에서 어떤 확률변수 X를 r번째 성공을 얻을 때까지 걸리는 시행횟수라고 할 때, X를 음이항확률변수라고 하고 그 분포를 음이항분포라고 한다.

 

 

'음'이항분포라는 이름에서 알 수 있듯 이항분포와 반대되는 개념이다. 전체 시행횟수를 n, 성공횟수를 r이라고 할 때, 이항분포에서는 시행횟수 n이 고정되어 있고 성공횟수 r이 확률변수이다. 이에 반해 음이항분포에서는 시행횟수 n이 확률변수이고 성공횟수 r이 고정되어 있다.

 

ex)

7번의 경기 중 4번을 먼저 승리해야 할 때 A팀이 6번째 경기에서 우승할 확률은?

 

이 예시에서 A팀이 6번째 경기에서 우승하려면 이전의 5개의 경기 중 3승 2패를 해야한다. 즉, 성공횟수 r=4는 고정되어 있고 시행횟수가 확률변수인 것이다.

 

 

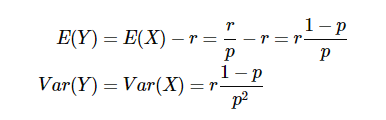
추가로 음이항분포의 확률질량함수에서 r=1이면 기하분포의 확률질량함수와 같아진다.

 

 

또 음이항분포는 이항분포와 마찬가지로 포아송 분포로 수렴된다는 특징이 있다. 성공횟수가 무한대로 커지고 실패 확률이 매우 작아지면서 곱이 람다에 수렴하게 될 경우 음이항분포는 포아송분포에 수렴하게 된다. 반대로 이항분포는 전체 시행횟수가 무한히 커기고 성공확률이 매우 작아지면서 곱이 람다에 수렴하면 포아송분포에 수렴한다.

 

 

4. 다항분포

 

다항분포는 여러 개의 값을 가질 수 있는 독립확률변수들에 대한 확률분포로 여러 번의 독립적 시행에서 각각의 값이 특정 횟수가 나타날 확를을 정의한다. 다항 분포에서 차원이 2인 경우가 바로 이항분포이다.

 

 

즉, 결과가 성공 실패 2개의 결과만 있는 경우가 이항분포, 발생 결과가 3개 이상인 경우는 다항분포이다.